Mathematics used to be a lot more important for game development than it is now. There are so many tools available for creating all kinds of things so we don’t have to do the math ourselves. Besides that, many types of games don’t require much math in the first place. So a game programmer can go a long way with almost no math.
But if you can do some math, it can be very useful, especially for procedural techniques and special effects. Below are what I believe the best books covering topics relevant to games.
I left out two broad topics: calculus and statistics. Both those are also useful in games, but less often and in more specific contexts.
Foundations of Game Engine Development, Volume 1: Mathematics
— Eric Lengyel
This concise book has four chapters, arranged in order of importance. The first three chapters are essential reading. They deal with vectors, matrices, transformations, and geometry. The material on vectors, matrices, and transformations is solid, but the geometry chapter is a bit light. Even so, its section on normals transformation would have saved me a lot of time the first time I had to do one.
The final chapter is a treat; it deals with projective geometry, and other types of algebra that makes geometry more elegant, and illuminates curiosities such as why the cross product only exists in certain dimensions. Although it is interesting, this is unlikely to be useful to the typical game developer.

Real-time collision detection
— Christer Ericson
Although this is not strictly a mathematics book, the bulk of the content is about geometry, and this is a great book to learn about geometric programming. Despite the title, many of the algorithms are useful in other contexts (such as navigation, for example).
What I really like about this book is that it is very practical — it does not gloss over the issues you will face when you write an actual program. There are chapters on geometrical robustness, and optimization, which are very useful if you write real code.
Geometric Tools for Computer Graphics
— Philip J. Schneider and David H. Eberly
This tome is a very useful reference that contains hundreds of algorithms. It discusses many recurring geometric problems: finding distances, intersections, projections, angles, normals between or of various primitives. It also discusses some other topics such as space partitioning, point in polygon or polyhedra tests, and Boolean operations on polygons and polyhedra (a topic not covered in many books).

Essential Mathematics for Games and Interactive Applications: A Programmer’s Guide
— Max K. Agoston
This book covers a wide variety of topics related to rendering, including projection, lighting and shaders, and rasterization.
There are also some chapters on physics, random numbers, and interpolation. There is a good chapter discussing the intricacies of floating-point numbers.
Practical Linear Algebra: A Geometry Toolbox
— Gerald Farin and Dianne Hansford
Most linear algebra books (and I guess university courses) focus on the algebraic aspect of linear algebra. This viewpoint is of limited use to game developers. But this book is centered around geometry. It covers a large number of topics, including 2D and 3D triangulations, barycentric coordinates, lightning and shading, homogeneous coordinates, polygons, Bézier curves, and many more.
It also covers the “usual” linear algebra topics such as eigenvectors and determinants. But the book shows you their geometric interpretation.

Discrete and Computational Geometry
— Satyan L. Devadoss and Joseph O’Rourke
This book beautiful — very visual. It covers more advanced geometric algorithms dealing with triangulations, Voronoi diagrams, curves, and polyhedra. It is a bit more theoretical than some of the other algorithm books listed here, but it has compact algorithm descriptions (with time complexity shown) that is useful to reference. This is the right book to get a solid base if you do a lot of geometric coding.

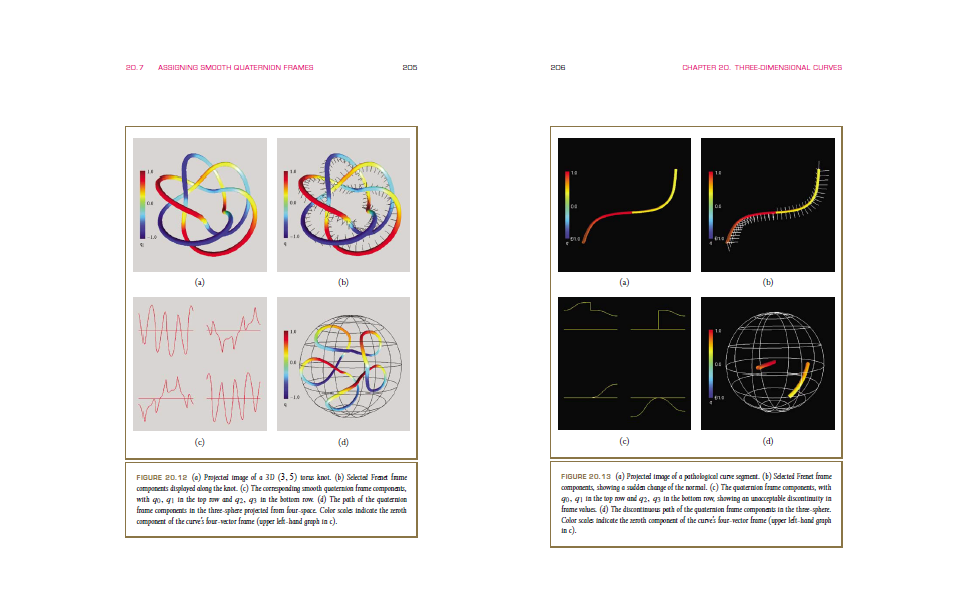
Visualizing Quaternions
— Andrew J. Hanson
The sections on quaternions in Foundations of Game Engine Development, Volume 1 are sufficient for practical purposes. Unfortunately, most books that delve deeper into quaternions are either very mathematical (using concepts from abstract algebra), or very confusing. This book falls into the latter category, and sometimes it is difficult to understand what the author means.
However, if you can fill in the blanks, this book covers many interesting topics. It gives you four different viewpoints, that are helpful for understanding quaternions and rotations more intuitively. It also considers some applications (such as orientation along 3D curves and surfaces) in a lot of depth.