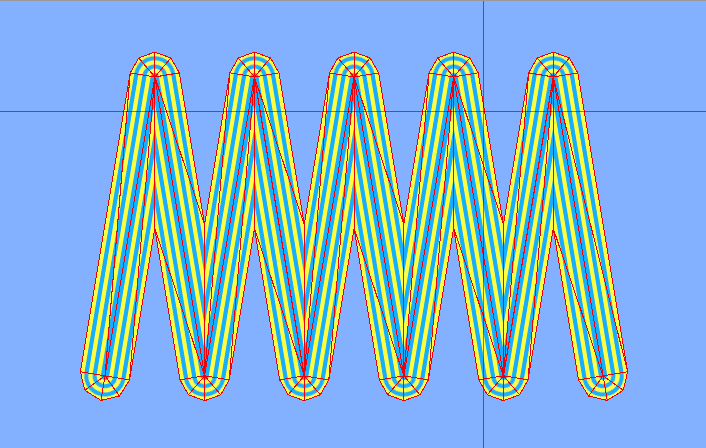
A lines is a fundamental graphics object, but generating attractive, robust lines involve many subtle issues and can be difficult to get right.
In this post I show some examples of rolling out your line meshes. To develop a full-fledged multi-purpose line solution is a big project, in practice you will usually build a solution closely tailored for your application. Here we will look at a few specific-purpose solutions to go over some of the main concepts. You should be able to put these together into something that is suitable for your own use-cases.
This post builds on Generating procedural meshes in Unity. Since writing that post, I realized I missed some steps in the process I proposed.
Here are the steps used here:
- Draw a picture!
- Specify the parameters of the problem, that is, the thing you will want to specify, such as the line thickness.
- Identify problematic cases. I describe some of these in the next section. Although I list it as step 2, in reality you will spot most of them only as you work through the other steps. That said, giving it some thought before you start with the calculations will prime your brain so you can be on the lookout.
- … (same as before)
However, when we break down our calculations into primitives, we follow a different path from step 4 onwards. Here are the steps I used to design the mesh builders for this post:
- Draw a picture!
- Specify the parameters of the problem.
- Identify problematic cases.
- Identify the primitives we will use.
- Calculate the parameters of the primitives.
I also realized the “trianglesPerRad” is a silly metric to use since it is so hard to visualize radians. Instead, use trianglesPerRevolution. I always start with raw triangleCount for sectors, and convert that to a calculated amount once the whole thing is working.
Problematic Cases
Geometric code always have lots of annoying cases where the naive solutions breaks down. It is not uncommon to have more “special case” code than normal case code. It is especially tricky because it is hard to exhaust all the special possibilities.
When it comes to line code, here are some situations that can cause problems.
Too few points. For example, the broken line mesh builder below checks for intersections of two lines parallel to consecutive segments, which means at least three points is required. Special code is required if there are fewer than three points. You can usually see this situation easily in code
for(i = 0 ... count – k) func(points[i], points[i + 1], ..., points[i + k]) //requires at least k + 1 points. </p>
Points that are too close. This is a problem if we need the direction of the segment between the two points, for example, to calculate a perpendicular.
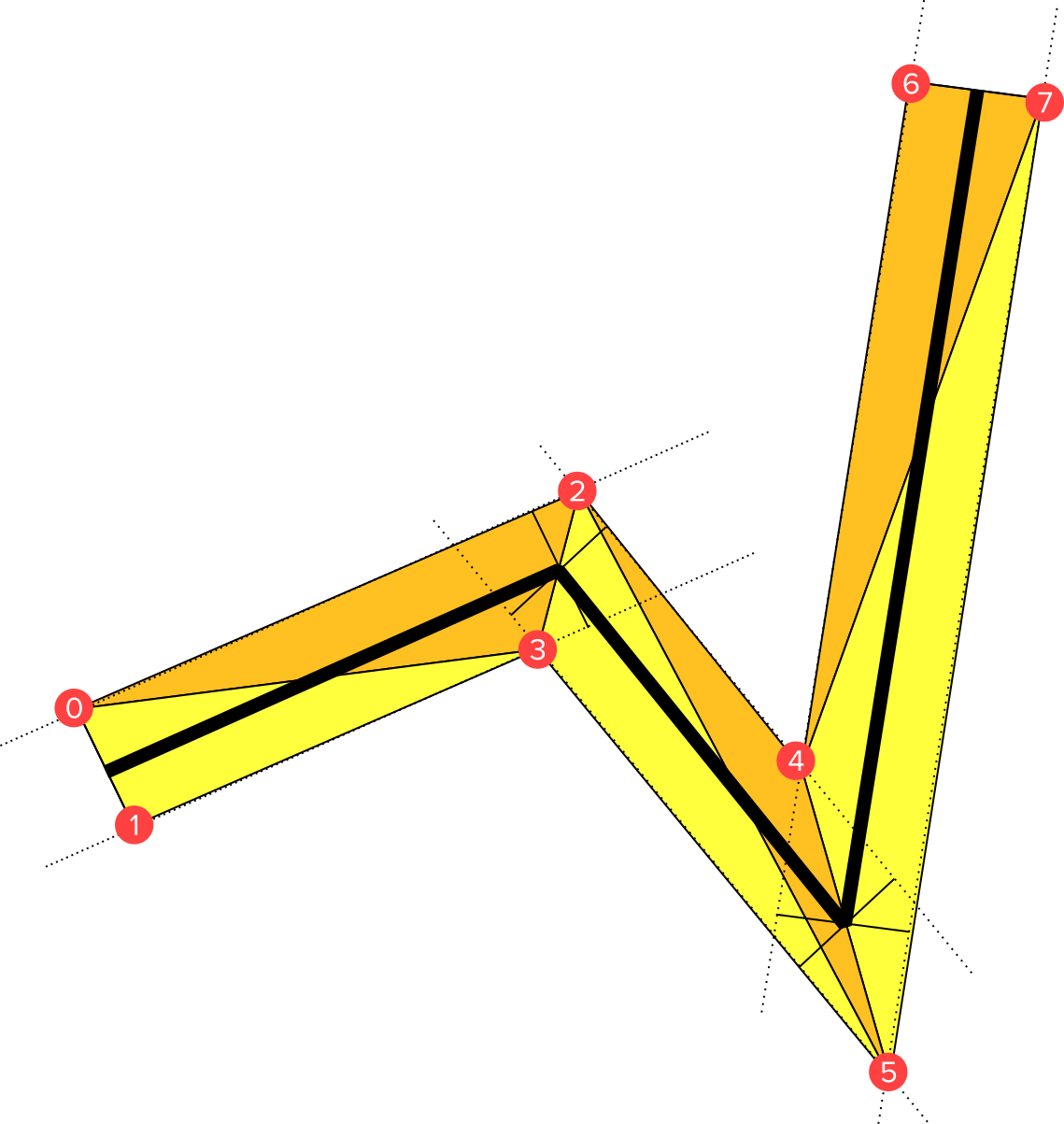
Intersections of lines that are too parallel. Parallel lines either don’t intersect, or they coincide. In either case, the intersection is not useful, and we need special code to handle parallel lines. Even when lines are merely almost parallel can cause problems – the intersection may be a point very far from the area we are interested in (for example, too far from the camera). In broken line mesh builders, there are two cases of almost parallel: a vertex whose adjacent segments makes an angle of almost 180 degrees, and a vertex whose adjacent segments makes an angle of almost 360 degrees. The first case is much easier handled (we can make a stand-in intersection perpendicular to the segments). The second case needs special code (and in fact, that code is fairly complicated and not given here).
Lines are very thick. Thismay cause lines to overlap themselves in unexpected ways, messing up the triangulation.
Points very far apart. I thought that very long lines might also cause problems, but it seems Unity handles lines 10000 units long and 0.01 units thick fine.
Primitives
We will be using some generic methods to generate shapes we use across multiple builders: quads and sectors. We looked at both of these in the previous post.
Architecture
In the previous post, I used a base class that was suitable for building simple meshes. However, it is not great for meshes made from different parts. Instead, these are the main classes to support the builders for this post. Sourcecode is given at the end.
MeshDatais a simple class with all the data we need: vertices, triangles, UVs and normals. It also has a Compose method that allows you to compose a list ofMeshDatainstances into a single one.MeshDataMeshBuilderis a new base class suitable for combined meshes. Instead of requiring you to override different methods for vertices, triangles, and so on, you only have to implement a single method that returns everything in aMeshDataobject. (This class extends the original base classMeshBuilder.)MeshBuilderUtilscontains code to generate sectors and quads, as well as other helpers, mostly to do geometry.GeometryDebugis a new class that handles the display of debugging information (points and arrows). You normally don’t work with this class directly, but instead with methods provided inMeshBuilder.
(This is still not the setup I will use for a library. I would prefer to be able to have MeshData objects for primitive shapes, and compose those using a generic builder. That is for a future post.)
Line Mesh Builders
Here we will look at three types of line builder:
- A single segment with round ends.
- A broken line with nice (sharp) joins.
- A broken line with nice joins (round for convex corners and sharp for concave corners)
A line segment with round end points
A line segment with round corners is simply a long thin rectangle with two half-circles stuck onto two opposite sides, which means we could use the square and circular sector meshes of the previous post if we wanted to. Here we will do it from scratch, although the thinking is the same as for the previous meshes.
Decide on the parameters: Two endpoints (point0 and poin1), width, triangleCount.
Potential Special Cases: Two end points are too close; thickness is 0.
Decide on primitives: Two sectors and a quad.
Calculate parameters of primitives:
- Sector 0: center at point0, radius is half-width, start angle is 90 degrees CCW from segment angle, end angle is 270 degrees from segment angle.
- Sector 1: center at point 1, radius is half-width, start angle is 270 CCW from the segment angle, end angle 90 is degrees from segment angle.
- Quads: The endpoints of four perpendiculars raised on the segment at the endpoints, each of length half the width.
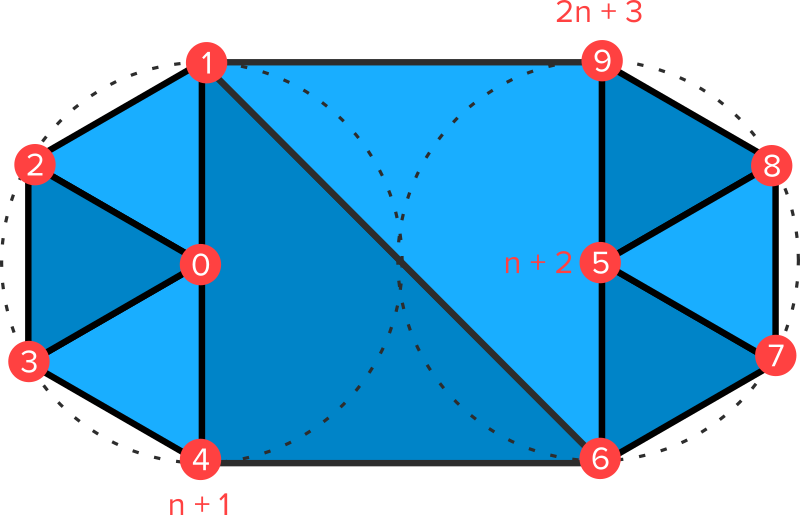
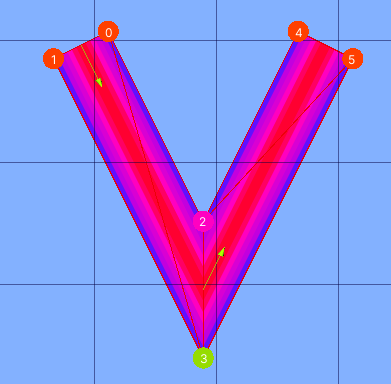
Broken line segment with sharp joins
Form a series of points that represent consecutive line segments, we make a shape as follows: For each segment, we raise two perpendiculars, one on each side of the segment, half the line width. Through these, we find two lines parallel to the segment, one on each side. The points where consecutive lines on the same side of the broken line intersect are the join vertices. For the end points, we use the perpendiculars raised at the end points and half the line width.
Decide on the parameters: points that represent the nodes of the line (i.e. end points of segments that make up the line) and line width.
Potential Special Cases: Two consecutive points are too close; thickness is 0, consecutive segments are too parallel.
Assign vertices: We do it as shown in the image.
Calculate the vertices: This is explained in the paragraph above. If the angle between consecutive segments is almost 180 degrees, we use tops of perpendicular instead of intersection points. The other near-parallel case (when the segments form an angle of almost 0) is not handled. I fix is possible, but would be difficult, and I did not attempt it.
Calculate the number of vertices: 2 * pointCount.
Calculate the triangles: Each segment of the broken line is made of two triangles
- 2i + offset, 2i + offset + 1, 2i + offset + 3 and
- 2i + offset, 2i + offset + 2, 2i + offset + 3
Calculate the number of triangles: 2 * (pointCount – 1)
Calculate the UVs. The simplest idea is to use only two UVs: (0.5, 0) for bottom vertices and (0.5, 1) for top vertices. We can also calculate stretch the texture proportionally over the line by using the following UVs: (u_i, 0) for bottom and and (u_i, 1) for top, where
u_i = lengthUpToVertex_i / totalLength
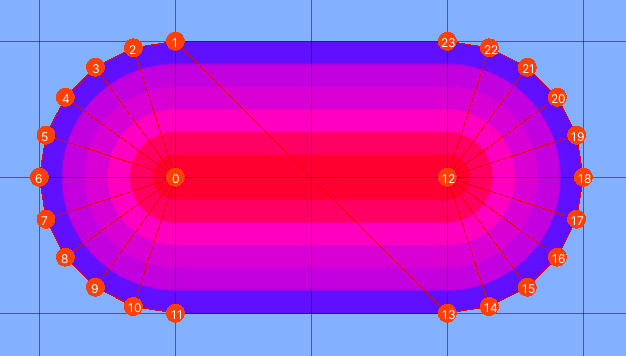
Line with Round Joins
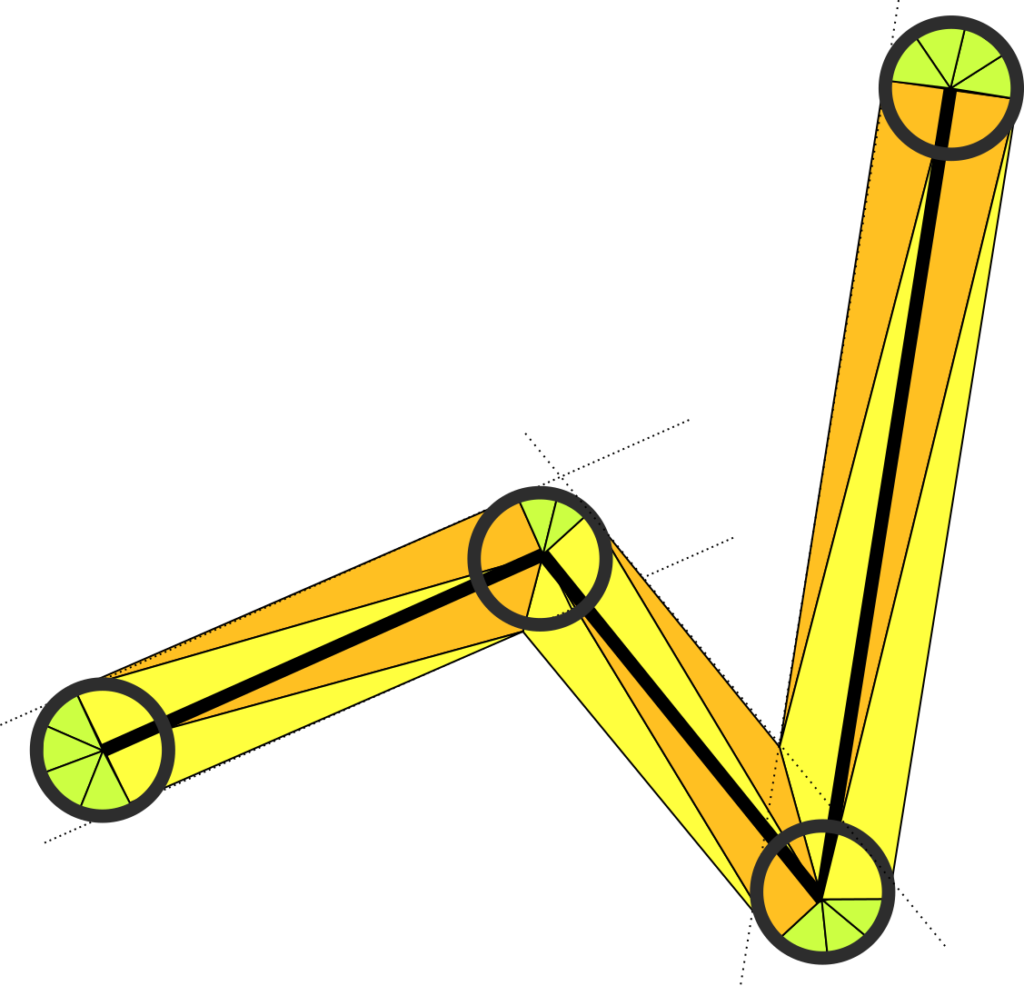
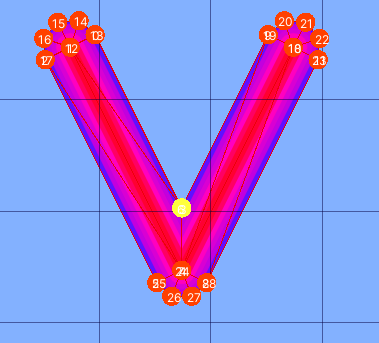
This line is much more complicated to generate. It follows the same idea as the previous mesh builder; we calculate intersections as before. But we do not use this for both top and bottom vertex. If one of them is convex, we replace the corner there with a circular sector, as shown in the picture below.
We break the mesh down into quads and sectors. As you can see, for the non-looping version, there is two quads per segment (this 2(pointCount – 1)), and one sector per point (this includes two sectors at the end points). Notice that the two vertical segments of each quad is either from point to intersection, or from point the top of a perpendicular raised at that point. The sectors also all lie between perpendiculars raised on the points. This gives as all the information we need to calculate the shapes; the trick is to keep track of whether to use the sector at the top or bottom (if at all).
Parameters: points, width, triangleCount (for sectors)
Potential special cases: same as before.
Decide on primitives: Sectors at each end point, a sector at each convex join vertex, and two quads per segment.
Calculate parameters of primitives: Each sector has its center at a input point, and lies between perpendiculars at these points, the start and end angles are the angles of these perpendiculars. The radius of all sectors are width / 2. Note that all sectors lie between perpendiculars on the same side of the line, except the sectors at the end points.
Each quad has two corners made from the input points, and the remaining two points are either points of intersection (the same points of intersection calculated in for the broken line with sharp joins), or the top of a perpendicular. The tricky part is to keep track of which we should use for a particular quad. There are some details for special cases, but the overall test is done by taking the perp-dot product of consecutive segments, and see whether they are positive or negative. This essentially tells us whether the second segment lies to the left or right of the first segment, and therefor whether the angle between them is obtuse or not, and therefor whether the top or bottom join vertex is convex.
More Implementation Tips
Use degrees in the inspector and radians internally. It is hard to visualize the size of radians, and you cannot easily specify special angles such as 90 or 60 degrees. But internally (for math calculations, it makes more sense to stick to radians. My convention is to add inDegrees to variables that represent angles in degrees. I only use inRadians for angles that have both an inDegrees and inRadians versions.
Consider keeping looping and non-looping implementations separate. It is sometimes easier to develop the looping and non-looping versions of a mesh builder separately, keeping them together with appropriate is a brain tax you don’t need to pay. Once you have both working, you may refactor so that shared code is not duplicated, but even then I am not sure it is a good idea. The branching can make the code much harder to understand.
To convert non-looped to looped:
- Remove the set of start and end vertices (including the start and end caps).
- Calculate an extra set of in-between vertices (between last and first point). In practice you can run extra iterations in the loop (making sure to wrap indices back).
- Remove triangles of the start and end caps.
- Remove triangles from the (original) first set of vertices (those vertices are no gone, remember). In practice this is a suitable offset inside the loop. This part is easy to overlook and may result in triangles that have no area and are therefore not visible.
- Add extra rectangles for the mesh between the last and first points. In practice, this is executing the loop for extra an iteration, wrapping indices back.
The process is not completely general, you have to analyze it for your specific case.
For more advanced meshes, add additional debug options. Inaddition to showing vertices, you may also want to show:
- Vertex indices. I am always surprised how easy it is for my mental picture of geometry to be different from reality in subtle ways – maybe I swapped X and Y, or coordinates are reflected vertically, or a set of points go anti-clockwise when I think they go clockwise. These mental models invariably lead to incorrect implementations (and these can be hard to debug, since the real bug is in your brain and not the code.) Seeing where everything is can flush these types of misconceptions out in a few seconds.
- Interim calculated positions or directions. You can verify correct math a lot easier visually. For example, you can at a glance see if a calculated point of intersection is where the entities intersect, or whether a direction really is perpendicular to some other direction. And visual cues can be helpful to understand how the code could be wrong.
Do not try to make the code as general as possible (unless you are writing a library for other programmers). Writing robust geometric code is exceptionally hard. If your game is 2D, then make your code only work in 2D. If you know all your points are “nice”, don’t cater for non-nice situations. If you know your code will always generate at least three points for a line, don’t worry about degenerate cases. If you only need loops, don’t implement non-loops.
That said, if you can spot problematic cases:
- Add a comment in the code describing the situation, and the consequences.
- If it is easy to test for this case, test it and throw an error if it occurs. You are still not solving it, but at least the code user (your future self) will be notified if the code is being used inappropriately.
Do not try to share every vertex that is shareable unless you have to. In our line builder with round joints above we broke the line up into multiple components. This made the code much easier to write. The downside is there are a few redundant vertices, which in theory is somewhat slower. (You will have to work though to see the difference.) Even if you need a super-efficient implementation, it’s always better to start with a correct (potentially unoptimized) version that can be used as a reference implementation for something faster. And a correct version may also be easier to modify into a faster version than trying to build it directly:
- You can (somewhat) easily see where you can reduce the vertices, and how to adjust counts to make triangles still work. (These counts are the things that trip you up if you try to do it directly).
- You can implement an algorithm that will identify certain vertices by removing duplicates and adjusting triangle arrays accordingly. This too may be easier than to figure out the correct counts right from the beginning.
Give thoughtful variable names. The mathy nature of geometric code can dupe programmers to give math style names – single letter names – which makes the code more compact, but harder to understand. And it can be tricky to name intermediate calculations. Here is my approach to naming in this type of code. (Note, my code is consumed by our small team. Code meant for a wider audience need to have an even more robust naming strategy.
- Acceptable one-letter variable names.
x,y,zfor coordinates
i,j,kfor vanilla loop counters (I try to always use vanilla loops, but if I don’t, I will use something more descriptive that reflects the loop counter’s role in the code, such as “triangleOffset”)
tfor a parameter (similar to t in Lerp and gradient.Evaluate)
uandvfor texture coordinates
- Use mathematical terminology when appropriate: corner, center, direction, intersection, determinant, discriminant, diagonal, sector, arc, segment, radius, and so on.
- Use visual cues from your drawings. For example, in my drawing of the line mesh, there is a “top” and “bottom”, with top and bottom lines, and top and bottom intersections. I have even found it helpful in complicated situations to use colors to help me keep track:
blueSegmentand redSegment (where those correspond to the colors in my drawing). While this is a great help during implementation, it may be confusing for anyone who does not have access to the drawing. You have a few options:- You can put the drawing in an accessible spot (such as a company wiki or the software docs), and that will be fine. This is the right way to go if there is a spot where the team (including you) access information already.
- The terms can be defined, and this is what comments are for. “In the implementation below, a vertex is either red, blue or green. Red vertices …” At times writing these definitions explicitly suggests better names, in which case you can rename the variables.
- You can find a better name if you look hard enough. The concepts we encounter in everyday game development are seldom new. There must be thousands of books that talk about lines and their rendering. The name you are looking for is out there.
- When none of the above yield anything useful, use a simple direct, easily digestible name, and explain your algorithm in a comment.
- Be specific. Use names to help distinguish between indices, vertices, directions, dimensions, and so on.
Test for (almost) zero-area triangles. Test the area of each triangle once it is created, and make sure it is above a threshold. Print a debug message or throw an error with the vertex indices and coordinates of very small triangles. This will help flush out three classes of errors:
- Providing the algorithm with degenerate inputs.
- Errors caused by incorrect triangle calculations.
- Errors caused by incorrect vertex calculations.
The area of a triangle ABC is given by half the magnitude of the cross product of vectors AB and AC.
public static float AreaOfTriangle(Vector3 sideAB, Vector3 sideAC)
{
return 0.5f * Vector3.Cross(sideAB, sideAC).magnitude;
}
Code
MeshBuilder
using System.Collections.Generic;
using System.Linq;
using UnityEditor;
using UnityEngine;
public enum MeshType{
XYZ,
XY,
XZ
}
[RequireComponent(typeof(MeshFilter))]
public class MeshBuilder: MonoBehaviour
{
private readonly static Color DebugSphereColor = new Color(1, 0.25f, 0);
private const float SmallestValidTriangleArea = 0.01f;
[Header("Debug Options")]
[SerializeField]
private bool drawDebugVertices = false;
[SerializeField]
private bool drawDebugLabels = false;
[SerializeField]
private bool printDebugInfo = false;
[SerializeField]
private float debugSphereRadius = 0.1f;
[SerializeField]
private MeshType meshType = MeshType.XYZ;
//Use property instead to ensure initialization
private MeshFilter meshFilter;
//We keep this as a variable so we can draw debug Info
private List<Vector3> vertices;
private GUIStyle vertexLabelStyle;
[HideInInspector]
[SerializeField]
protected GeometryDebug meshDebug;
protected MeshFilter MeshFilter
{
get
{
if (meshFilter == null)
{
meshFilter = GetComponent<MeshFilter>();
//cannot be null since MeshFilter is required.
}
return meshFilter;
}
}
public void UpdateMesh()
{
if (meshDebug == null)
{
meshDebug = new GeometryDebug();
}
meshDebug.Clear();
DestroyOldMesh();
Preprocess();
var mesh = new Mesh();
vertices = CalculateVertices();
DebugLog("Vertices", vertices.Count);
mesh.SetVertices(vertices);
var triangles = CalculateTriangles();
DebugLog("Triangles", triangles.Count);
mesh.SetTriangles(triangles, 0);
//We set triangles before doing this test so that the number of
//vertex indices and their range can be checked before we execute
//the code below, that will
ValidateTriangleAreas(triangles);
var uvs = CalculateUvs(vertices);
if (uvs == null)
{
//can be null if subclass does not support texturing
DebugLog("Uvs", null);
}
else
{
DebugLog("Uvs", uvs.Count);
mesh.SetUVs(0, uvs);
}
var normals = CalculateNormals();
if (normals == null)
{
//can be null if subclass does override default normals
DebugLog("Normals", null);
mesh.RecalculateNormals();
}
else
{
DebugLog("Normals", normals.Count);
mesh.SetNormals(normals);
}
mesh.RecalculateBounds();
meshFilter.sharedMesh = mesh;
}
private void ValidateTriangleAreas(List<int> triangles)
{
for (int i = 0; i < triangles.Count / 3; i++)
{
int vertexIndexA = triangles[3 * i];
int vertexIndexB = triangles[3 * i + 1];
int vertexIndexC = triangles[3 * i + 2];
var vertexA = vertices[vertexIndexA];
var vertexB = vertices[vertexIndexB];
var vertexC = vertices[vertexIndexC];
float area = MeshBuilderUtils.AreaOfTriangle(vertexB - vertexA, vertexC - vertexA);
if (area < SmallestValidTriangleArea)
{
Debug.LogWarning(
string.Format(
"Triangle is too small. <{0}, {1}, {2}>, <{3}, {4}, {5}>",
vertexIndexA, vertexIndexB, vertexIndexC, vertexA, vertexB, vertexC
));
}
}
}
public void OnDrawGizmos()
{
if (!drawDebugVertices && !drawDebugLabels) return;
if (vertices == null) return; //can happen if no mesh was ever created.
//if(vertexLabelStyle == null)
{
vertexLabelStyle = new GUIStyle();
vertexLabelStyle.normal.textColor = Color.white;
vertexLabelStyle.alignment = TextAnchor.MiddleCenter;
}
if(drawDebugVertices)
{
meshDebug.Radius = debugSphereRadius;
for (int i = 0; i < vertices.Count; i++)
{
var vertex = vertices[i];
var spherePosition = transform.TransformPoint(vertex);
float radius = transform.lossyScale.magnitude * debugSphereRadius;
GeometryDebug.DrawDot(spherePosition, radius, DebugSphereColor, meshType);
}
if (meshDebug != null)
{
meshDebug.Draw(transform, meshType);
}
}
if(drawDebugLabels)
{
for (int i = 0; i < vertices.Count; i++)
{
var vertex = vertices[i];
var spherePosition = transform.TransformPoint(vertex);
float radius = transform.lossyScale.magnitude * debugSphereRadius;
Handles.Label(spherePosition + Vector3.up * radius / 2, i.ToString(), vertexLabelStyle);
}
}
}
virtual protected List<Vector3> CalculateVertices()
{
return MeshBuilderUtils.QuadVertices();
}
virtual protected List<Vector2> CalculateUvs(List<Vector3> vertices)
{
return MeshBuilderUtils.GetStandardUvsXY(vertices, true, true);
}
virtual protected void Preprocess() { }
virtual protected List<int> CalculateTriangles()
{
return new List<int>
{
0, 3, 1,
1, 3, 2
};
}
virtual protected List<Vector3> CalculateNormals()
{
return null;
}
[ContextMenu("Update Mesh")]
protected void UpdateMeshTest()
{
UpdateMesh();
}
private void DestroyOldMesh()
{
if (MeshFilter.sharedMesh != null)
{
if (Application.isPlaying)
{
Destroy(MeshFilter.sharedMesh); //prevents memory leak
}
else
{
DestroyImmediate(MeshFilter.sharedMesh);
}
}
}
protected void DebugLog(string label, object message)
{
if (!printDebugInfo) return;
if (message == null)
{
DebugLog(label, "null");
}
else
{
Debug.Log(label + ": " + message.ToString(), this);
}
}
protected void DebugAddDotXY(Vector3 position, GLColor color)
{
meshDebug.AddDotXY(position, color);
}
public void DebugAddArrow(Vector3 position, Vector3 direction, GLColor color)
{
meshDebug.AddArrow(position, direction, color);
}
private void GetVerticesFromMesh()
{
if (MeshFilter.sharedMesh != null)
{
vertices = MeshFilter.sharedMesh.vertices.ToList();
DebugLog("Vertices", "Refreshed from mesh.");
}
}
private void OnValidate()
{
if(vertices == null)
{
GetVerticesFromMesh();
}
}
}
MeshDataMeshBuilder
using System.Collections.Generic;
using UnityEngine;
public class MeshDataMeshBuilder : MeshBuilder
{
private MeshData meshData;
virtual protected MeshData GetMeshData()
{
return new MeshData();
}
protected override void Preprocess()
{
meshData = GetMeshData();
}
sealed protected override List<Vector3> CalculateVertices()
{
return meshData.vertices;
}
sealed protected override List<int> CalculateTriangles()
{
return meshData.triangles;
}
sealed protected override List<Vector3> CalculateNormals()
{
return meshData.normals;
}
sealed protected override List<Vector2> CalculateUvs(List<Vector3> vertices)
{
return meshData.uvs;
}
}
SegmentMeshBuilder
using System.Collections.Generic;
using UnityEngine;
public class SegmentMeshBuilder : MeshBuilder
{
[Header("Mesh Options")]
public Vector3 point0;
public Vector3 point1;
[Min(0)]
public float width;
[Min(0)]
public int trianglesPerRevolution;
private int c0Index;
private int c1Index;
private int p0Index;
private int q0Index;
private int triangleCount;
protected override void Preprocess()
{
//triangles in semicircle
triangleCount = Mathf.CeilToInt(0.5f * trianglesPerRevolution);
c0Index = 0;
p0Index = 1;
c1Index = triangleCount + 2;
q0Index = triangleCount + 3;
}
protected override List<Vector3> CalculateVertices()
{
var vertices = new List<Vector3>();
vertices.AddRange(MeshBuilderUtils.SectorVertices(point0, width / 2, MeshBuilderUtils.Right1, MeshBuilderUtils.Right3, true, triangleCount));
vertices.AddRange(MeshBuilderUtils.SectorVertices(point1, width / 2, MeshBuilderUtils.Right3, MeshBuilderUtils.Right1, true, triangleCount));
return vertices;
}
protected override List<int> CalculateTriangles()
{
var triangles = new List<int>();
triangles.AddRange(MeshBuilderUtils.SectorTriangles(c0Index, triangleCount, true));
triangles.AddRange(MeshBuilderUtils.SectorTriangles(c1Index, triangleCount, true));
triangles.AddRange(MeshBuilderUtils.QuadTriangles(
p0Index, p0Index + triangleCount,
q0Index, q0Index + triangleCount));
return triangles;
}
protected override List<Vector2> CalculateUvs(List<Vector3> vertices)
{
var uvs = new List<Vector2>();
var center = Vector2.one / 2;
uvs.AddRange(MeshBuilderUtils.SectorUvs(center, 0.5f, MeshBuilderUtils.Right1, MeshBuilderUtils.Right3, triangleCount, true));
uvs.AddRange(MeshBuilderUtils.SectorUvs(center, 0.5f, MeshBuilderUtils.Right3, MeshBuilderUtils.Right1, triangleCount, true));
return uvs;
}
}
LineMeshBuilder
using System.Collections.Generic;
using System.Linq;
using UnityEngine;
using Gamelogic.Extensions;
public class LineMeshBuilder : MeshBuilder
{
public List<Vector3> points;
public bool loop;
[Min(0)]
public float width;
override protected List<Vector3> CalculateVertices()
{
float halfWidth = width / 2f;
var topLines = new List<Line>();
var bottomLines = new List<Line>();
int segmentCount = loop ? points.Count : (points.Count - 1);
Debug.Log(segmentCount);
for (int i = 0; i < segmentCount; i++)
{
int j = (i == points.Count - 1) ? 0 : i + 1;
var direction = (points[j] - points[i]).normalized;
meshDebug.AddArrow(points[i], direction, GLColor.Green);
var left = direction.PerpXY();
var top = points[i] + halfWidth * left;
var bottom = points[i] - halfWidth * left;
topLines.Add(new Line { offset = top, direction = direction });
bottomLines.Add(new Line { offset = bottom, direction = direction });
}
var vertices = new List<Vector3>();
for (int i = 0; i < points.Count; i++)
{
int j = (i == 0) ? points.Count - 1 : i - 1;
if ((i == 0) && !loop)
{
vertices.Add2(topLines[i].offset, bottomLines[i].offset);
}
else if ((i == points.Count - 1) && !loop)
{
var direction = topLines[j].direction;
var left = direction.PerpXY();
var top = points[i] + halfWidth * left;
var bottom = points[i] - halfWidth * left;
vertices.Add2(top, bottom);
}
else if (MeshBuilderUtils.IsParallel(topLines[i], topLines[j]))
{
Debug.Log("Parallel");
vertices.Add2(topLines[i].offset, bottomLines[i].offset);
}
else
{
var topIntersection = MeshBuilderUtils.GetIntersection(topLines[i], topLines[j]);
var bottomIntersection = MeshBuilderUtils.GetIntersection(bottomLines[i], bottomLines[j]);
meshDebug.AddDotXY(topIntersection, GLColor.Magenta);
meshDebug.AddDotXY(bottomIntersection, GLColor.Green);
vertices.Add2(topIntersection, bottomIntersection);
}
}
return vertices;
}
override protected List<int> CalculateTriangles()
{
int segmentCount = loop ? points.Count : points.Count - 1;
var triangles = new List<int>();
for (int i = 0; i < segmentCount; i++)
{
int j = (i == points.Count - 1) ? 0 : i + 1;
triangles.AddRange(
MeshBuilderUtils.QuadTriangles(
2 * i + 0,
2 * i + 1,
2 * j + 1,
2 * j + 0
)
);
}
return triangles;
}
override protected List<Vector2> CalculateUvs(List<Vector3> vertices)
{
var lengths = points.Differences((u, v) => (v - u).magnitude, loop);
float totalLength = lengths.Sum();
int segmentCount = loop ? points.Count : points.Count - 1;
var uvs = new List<Vector2>();
uvs.Add2(Vector2.zero, Vector2.up);
float accumulativeLength = 0;
for(int i = 0; i < points.Count - 1; i++)
{
accumulativeLength += lengths[i];
float u = accumulativeLength / totalLength;
uvs.Add2(new Vector2(u, 0), new Vector2(u, 1));
}
return uvs;
}
}
RoundLineMeshBuilder
using UnityEngine;
using System.Collections.Generic;
using Gamelogic.Extensions;
public class RoundLineMeshBuilder : MeshDataMeshBuilder
{
[Header("Mesh Options")]
public List<Vector3> points;
public float width;
public bool loop;
//public int triangleCount = 5;
public float trianglesPerRevolution = 12;
protected override MeshData GetMeshData()
{
List<MeshData> meshes = new List<MeshData>();
if (loop)
{
meshes.Add(CalculateQuadsLoop());
meshes.AddRange(CalculateJointFansLoop());
}
else
{
meshes.Add(CalculateQuads());
meshes.Add(CalculateStartCap());
meshes.Add(CalculateEndCap());
meshes.AddRange(CalculateJointFans());
}
return MeshData.Combine(meshes);
}
private MeshData CalculateQuads()
{
return new MeshData
{
vertices = CalculateQuadVertices(),
triangles = CalculateQuadTriangles(),
uvs = CalculateQuadUvs(false)
};
}
private MeshData CalculateQuadsLoop()
{
return new MeshData
{
vertices = CalculateQuadVerticesLoop(),
triangles = CalculateQuadTrianglesLoop(),
uvs = CalculateQuadUvs(true)
};
}
private List<Vector3> CalculateQuadVertices()
{
var vertices = new List<Vector3>();
var direction = (points[1] - points[0]).normalized;
var left = direction.PerpXY();
vertices.Add3(
points[0] + left * width / 2,
points[0],
points[0] - left * width / 2);
for (int i = 0; i < points.Count - 2; i++)
{
CalculateJoin(
points[i], points[i + 1], points[i + 2],
out bool fanAtTop, out Vector3 intersection,
out Vector3 fanStart, out Vector3 fanEnd);
if (fanAtTop)
{
vertices.Add3(fanStart, points[i + 1], intersection);
vertices.Add3(fanEnd, points[i + 1], intersection);
}
else
{
vertices.Add3(intersection, points[i + 1], fanStart);
vertices.Add3(intersection, points[i + 1], fanEnd);
}
}
int last = points.Count - 1;
direction = (points[last] - points[last - 1]).normalized;
left = direction.PerpXY();
vertices.Add3(
points[last] + left * width / 2,
points[last],
points[last] - left * width / 2);
return vertices;
}
private List<Vector3> CalculateQuadVerticesLoop()
{
var vertices = new List<Vector3>();
for (int i = 0; i < points.Count; i++)
{
var point0 = points[i];
var point1 = points[(i + 1) % points.Count];
var point2 = points[(i + 2) % points.Count];
CalculateJoin(
point0, point1, point2,
out bool fanAtTop, out Vector3 intersection,
out Vector3 fanStart, out Vector3 fanEnd);
if (fanAtTop)
{
Debug.Log(fanStart + " " + point1 + " " + intersection);
Debug.Log(fanEnd + " " + point1 + " " + intersection);
vertices.Add3(fanStart, point1, intersection);
vertices.Add3(fanEnd, point1, intersection);
}
else
{
Debug.Log(intersection + " " + point1 + " " + fanStart);
Debug.Log(intersection + " " + point1 + " " + fanEnd);
vertices.Add3(intersection, point1, fanStart);
vertices.Add3(intersection, point1, fanEnd);
}
}
return vertices;
}
private List<int> CalculateQuadTriangles()
{
var triangles = new List<int>();
for (int i = 0; i < points.Count - 1; i++)
{
int p0 = i * 6;
int p1 = i * 6 + 1;
int p2 = i * 6 + 2;
int p3 = i * 6 + 3;
int p4 = i * 6 + 4;
int p5 = i * 6 + 5;
triangles.AddRange(MeshBuilderUtils.QuadTriangles(p1, p4, p3, p0));
triangles.AddRange(MeshBuilderUtils.QuadTriangles(p2, p5, p4, p1));
}
return triangles;
}
private List<int> CalculateQuadTrianglesLoop()
{
var triangles = new List<int>();
int vertexCount = 6 * points.Count;
for (int i = 0; i < points.Count; i++)
{//+ 3 because we do not have the three points for the start cap
int p0 = (i * 6 + 0 + 3) % vertexCount;
int p1 = (i * 6 + 1 + 3) % vertexCount;
int p2 = (i * 6 + 2 + 3) % vertexCount;
int p3 = (i * 6 + 3 + 3) % vertexCount;
int p4 = (i * 6 + 4 + 3) % vertexCount;
int p5 = (i * 6 + 5 + 3) % vertexCount;
triangles.AddRange(MeshBuilderUtils.QuadTriangles(p1, p4, p3, p0));
triangles.AddRange(MeshBuilderUtils.QuadTriangles(p2, p5, p4, p1));
}
return triangles;
}
private MeshData CalculateStartCap()
{
var point0 = points[0];
var point1 = points[1];
var direction = (point1 - point0).normalized;
var left = direction.PerpXY();
var right = -left;
float startAngle = left.Atan2XY();
float endAngle = right.Atan2XY();
int triangleCount = Mathf.CeilToInt(0.5f * trianglesPerRevolution);
var vertices = MeshBuilderUtils.SectorVertices(
point0, width / 2, startAngle, endAngle, true, triangleCount);
var triangles = MeshBuilderUtils.SectorTriangles(0, triangleCount, true);
var center = Vector2.one / 2;
var uvs = MeshBuilderUtils.SectorUvs(center, 0.5f, MeshBuilderUtils.Right1, MeshBuilderUtils.Right3, triangleCount, true);
return new MeshData
{
vertices = vertices,
triangles = triangles,
uvs = uvs
};
}
private MeshData CalculateEndCap()
{
var point0 = points[points.Count - 2];
var point1 = points[points.Count - 1];
var direction = (point1 - point0).normalized;
var left = direction.PerpXY();
var right = -left;
float startAngle = left.Atan2XY();
float endAngle = right.Atan2XY();
int triangleCount = Mathf.CeilToInt(0.5f * trianglesPerRevolution);
var vertices = MeshBuilderUtils.SectorVertices(
point1, width / 2, startAngle, endAngle, false, triangleCount);
var triangles = MeshBuilderUtils.SectorTriangles(0, triangleCount, false);
var center = Vector2.one / 2;
var uvs = MeshBuilderUtils.SectorUvs(center, 0.5f, MeshBuilderUtils.Right3, MeshBuilderUtils.Right1, triangleCount, true);
return new MeshData
{
vertices = vertices,
triangles = triangles,
uvs = uvs
};
}
private List<MeshData> CalculateJointFans()
{
List<MeshData> meshes = new List<MeshData>();
for (int i = 0; i < points.Count - 2; i++)
{
CalculateJoin(
points[i], points[i + 1], points[i + 2],
out bool fanAtTop, out _,
out Vector3 fanStart, out Vector3 fanEnd);
float startAngle = (fanStart - points[i + 1]).Atan2XY();
float endAngle = (fanEnd - points[i + 1]).Atan2XY();
float revolutions = Mathf.Abs(MeshBuilderUtils.GetAngleBetween(startAngle, endAngle, !fanAtTop)) / MeshBuilderUtils.Right4;
int triangleCount = Mathf.CeilToInt(revolutions * trianglesPerRevolution);
var vertices = MeshBuilderUtils.SectorVertices(points[i + 1], width / 2, startAngle, endAngle, !fanAtTop, triangleCount);
var triangles = MeshBuilderUtils.SectorTriangles(0, triangleCount, !fanAtTop);
var center = Vector2.one / 2;
var uvs = MeshBuilderUtils.SectorUvs(center, 0.5f, startAngle, endAngle, triangleCount, !fanAtTop);
meshes.Add(new MeshData { vertices = vertices, triangles = triangles, uvs = uvs });
}
return meshes;
}
private List<MeshData> CalculateJointFansLoop()
{
List<MeshData> meshes = new List<MeshData>();
for (int i = 0; i < points.Count; i++)
{
var point0 = points[i];
var point1 = points[(i + 1) % points.Count];
var point2 = points[(i + 2) % points.Count];
CalculateJoin(
point0, point1, point2,
out bool fanAtTop, out _,
out Vector3 fanStart, out Vector3 fanEnd);
float startAngle = (fanStart - point1).Atan2XY();
float endAngle = (fanEnd - point1).Atan2XY();
float revolutions = Mathf.Abs(MeshBuilderUtils.GetAngleBetween(startAngle, endAngle, !fanAtTop)) / MeshBuilderUtils.Right4;
int triangleCount = Mathf.CeilToInt(revolutions * trianglesPerRevolution);
var vertices = MeshBuilderUtils.SectorVertices(point1, width / 2, startAngle, endAngle, !fanAtTop, triangleCount);
var triangles = MeshBuilderUtils.SectorTriangles(0, triangleCount, !fanAtTop);
var center = Vector2.one / 2;
var uvs = MeshBuilderUtils.SectorUvs(center, 0.5f, startAngle, endAngle, triangleCount, !fanAtTop);
meshes.Add(
new MeshData
{
vertices = vertices,
triangles = triangles,
uvs = uvs
});
}
return meshes;
}
public void CalculateJoin(
Vector3 p0, Vector3 p1, Vector3 p2,
out bool fanAtTop, out Vector3 intersection,
out Vector3 fanStart, out Vector3 fanEnd)
{
var direction0 = (p1 - p0).normalized;
var direction1 = (p2 - p1).normalized;
fanAtTop = PerpDotXY(direction0, direction1) < 0;
var left0 = direction0.PerpXY();
var left1 = direction1.PerpXY();
if (fanAtTop)
{
Line line0 = new Line { offset = p0 - width / 2 * left0, direction = direction0 };
Line line1 = new Line { offset = p1 - width / 2 * left1, direction = direction1 };
intersection = MeshBuilderUtils.GetIntersection(line0, line1);
meshDebug.AddDotXY(intersection, GLColor.Yellow);
fanStart = p1 + left0 * width / 2;
fanEnd = p1 + left1 * width / 2;
}
else
{
Line line0 = new Line { offset = p0 + width / 2 * left0, direction = direction0 };
Line line1 = new Line { offset = p1 + width / 2 * left1, direction = direction1 };
intersection = MeshBuilderUtils.GetIntersection(line0, line1);
meshDebug.AddDotXY(intersection, GLColor.Yellow);
fanStart = p1 - left0 * width / 2;
fanEnd = p1 - left1 * width / 2;
}
}
private float PerpDotXY(Vector3 v1, Vector3 v2)
{
return Vector3.Dot(v1.PerpXY(), v2);
}
private List<Vector2> CalculateQuadUvs(bool loop)
{
var uvs = new List<Vector2>();
int segmentCount = loop ? points.Count : (points.Count - 1);
for(int i = 0; i < segmentCount; i++)
{
uvs.Add3(new Vector2(0.5f, 1), new Vector2(0.5f, 0.5f), new Vector2(0.5f, 0));
uvs.Add3(new Vector2(0.5f, 1), new Vector2(0.5f, 0.5f), new Vector2(0.5f, 0));
}
return uvs;
}
}
Utility Classes
using Gamelogic.Extensions;
using System;
using System.Collections.Generic;
using System.Linq;
using UnityEditor;
using UnityEngine;
using UnityEngine.Assertions;
public class Line
{
public Vector3 offset;
public Vector3 direction;
public Vector3 Evaluate(float t)
{
return offset + direction * t;
}
override public string ToString()
{
return direction.ToString() + "[t]" + " + " + offset;
}
}
public class MeshData
{
public List<Vector3> vertices;
public List<int> triangles;
public List<Vector2> uvs;
public List<Vector3> normals;
public static MeshData Combine(List<MeshData> meshes)
{
MeshData combinedMesh = new MeshData
{
vertices = new List<Vector3>(),
triangles = new List<int>(),
uvs = new List<Vector2>(),
normals = new List<Vector3>()
};
int vertexIndexOffset = 0;
foreach(var mesh in meshes)
{
combinedMesh.vertices.AddRange(mesh.vertices);
combinedMesh.triangles.AddRange(mesh.triangles.Select(index => index + vertexIndexOffset));
if(mesh.uvs != null)
{
combinedMesh.uvs.AddRange(mesh.uvs);
}
if(mesh.normals != null)
{
combinedMesh.normals.AddRange(mesh.normals);
}
vertexIndexOffset += mesh.vertices.Count;
}
return combinedMesh;
}
}
public static class MeshBuilderUtils
{
private const float ParallelThreshold = 0.01f;
public const float Right1 = Mathf.PI / 2;
public const float Right2 = Mathf.PI;
public const float Right3 = 3 * Mathf.PI / 2;
public const float Right4 = 2 * Mathf.PI;
public static bool IsParallel(Vector3 direction0, Vector3 direction1)
{
return Vector3.Cross(direction0.normalized, direction1.normalized).magnitude < ParallelThreshold;
}
public static bool IsParallel(Line line0, Line line1)
{
return IsParallel(line0.direction, line1.direction);
}
private static Tuple<float, float> SolveLinearEquation(
float a0, float b0, float c0,
float a1, float b1, float c1
)
{
float v = (a1 * c0 - a0 * c1) / (a0 * b1 - a1 * b0);
float t = (-c0 - b0 * v) / a0;
return new Tuple<float, float>(t, v);
}
public static Vector2 Circle2(float angle)
{
return new Vector2(Mathf.Cos(angle), Mathf.Sin(angle));
}
public static Vector3 CircleXY(float angle)
{
return new Vector3(Mathf.Cos(angle), Mathf.Sin(angle), 0);
}
public static Vector3 GetIntersection(Line line0, Line line1)
{
Assert.IsTrue(!IsParallel(line0, line1), "Lines are (almost) parallel.");
var solutions = SolveLinearEquation(
Vector3.Dot(line0.direction, line0.direction),
-Vector3.Dot(line1.direction, line0.direction),
Vector3.Dot(line0.offset - line1.offset, line0.direction),
Vector3.Dot(line0.direction, line1.direction),
-Vector3.Dot(line1.direction, line1.direction),
Vector3.Dot(line0.offset - line1.offset, line1.direction)
);
var intersection = line0.Evaluate(solutions.Item1);
Debug.Log(intersection);
return intersection;
}
public static float GetAngleBetween(float startAngle, float endAngle, bool anticlockwise)
{
if (anticlockwise && endAngle < startAngle)
{
endAngle += Right4;
}
if (!anticlockwise && startAngle < endAngle)
{
startAngle += Right4;
}
float angleDifference = endAngle - startAngle;
return angleDifference;
}
public static float AreaOfTriangle(Vector3 sideAB, Vector3 sideAC)
{
return 0.5f * Vector3.Cross(sideAB, sideAC).magnitude;
}
public static List<Vector3> QuadVertices()
{
return new List<Vector3>
{
new Vector3(-1, 1, 0),
new Vector3(-1, -1, 0),
new Vector3(1, -1, 0),
new Vector3(1, 1, 0),
};
}
public static List<int> QuadTriangles(
int corner0,
int corner1,
int corner2,
int corner3
)
{
return new List<int>
{
corner0,
corner2,
corner1,
corner2,
corner0,
corner3,
};
}
public static List<Vector2> QuadUvs()
{
return new List<Vector2>
{
new Vector2(0, 1),
new Vector2(1, 1),
new Vector2(1, 0),
new Vector2(0, 0)
};
}
public static List<Vector3> SectorVertices(
float angle, int triangleCount)
{
return SectorVertices(Vector3.zero, 1, 0, angle, true, triangleCount);
}
public static List<Vector3> SectorVertices(
Vector3 center,
float radius,
float startAngle,
float endAngle,
bool anticlockwise,
int triangleCount)
{
var vertices = new List<Vector3>();
vertices.Add(center);
startAngle = GLMathf.FloorMod(startAngle, MeshBuilderUtils.Right4);
endAngle = GLMathf.FloorMod(endAngle, MeshBuilderUtils.Right4);
if (anticlockwise && endAngle < startAngle)
{
endAngle += MeshBuilderUtils.Right4;
}
if (!anticlockwise && startAngle < endAngle)
{
startAngle += MeshBuilderUtils.Right4;
}
float angleDifference = endAngle - startAngle;
float triangleAngle = angleDifference / triangleCount;
for (int i = 0; i < triangleCount + 1; i++)
{
float theta = triangleAngle * i + startAngle;
vertices.Add(center + radius * MeshBuilderUtils.CircleXY(theta));
}
return vertices;
}
public static List<int> SectorTriangles(
int start,
int triangleCount,
bool anticlockwise)
{
var triangles = new List<int>();
for (int i = 0; i < triangleCount; i++)
{
if (anticlockwise)
{
triangles.Add3(start, start + i + 2, start + i + 1);
}
else
{
triangles.Add3(start, start + i + 1, start + i + 2);
}
}
return triangles;
}
public static List<Vector2> SectorUvs(
Vector2 center,
float radius,
float startAngle,
float endAngle,
int triangleCount,
bool anticlockwise
)
{
var uvs = new List<Vector2>();
uvs.Add(center);
startAngle = GLMathf.FloorMod(startAngle, MeshBuilderUtils.Right4);
endAngle = GLMathf.FloorMod(endAngle, MeshBuilderUtils.Right4);
if (anticlockwise && endAngle < startAngle)
{
endAngle += MeshBuilderUtils.Right4;
}
if (!anticlockwise && startAngle < endAngle)
{
startAngle += MeshBuilderUtils.Right4;
}
float angleDifference = endAngle - startAngle;
float triangleAngle = angleDifference / triangleCount;
for (int i = 0; i < triangleCount + 1; i++)
{
float theta = triangleAngle * i + startAngle;
uvs.Add(center + radius * MeshBuilderUtils.Circle2(theta));
}
return uvs;
}
//Assumes a set of vertices in the XY plane
public static List<Vector2> GetStandardUvsXY(
List<Vector3> vertices,
bool preserveAspectRatio,
bool mapOriginToCenter
)
{
var boundingBox = GetBoundingBoxXY(vertices, mapOriginToCenter);
var map = GetStandardUvMapXY(boundingBox, preserveAspectRatio, mapOriginToCenter);
return vertices.Select(map).ToList();
}
private static Rect GetBoundingBoxXY(List<Vector3> vertices, bool mapOriginToCenter)
{
var anchor = vertices[0];
var extent = vertices[0];
foreach (var vertex in vertices.Skip(1))
{
if (vertex.x < anchor.x)
{
anchor.x = vertex.x;
}
else if (vertex.x > extent.x)
{
extent.x = vertex.x;
}
if (vertex.y < anchor.y)
{
anchor.y = vertex.y;
}
else if (vertex.y > extent.y)
{
extent.y = vertex.y;
}
}
if (mapOriginToCenter)
{
anchor.x = Mathf.Min(anchor.x, -extent.x);
anchor.y = Mathf.Min(anchor.y, -extent.y);
extent.x = Mathf.Max(extent.x, -anchor.x);
extent.y = Mathf.Max(extent.y, -anchor.y);
}
var size = extent - anchor;
return new Rect(anchor, size);
}
private static Func<Vector3, Vector2> GetStandardUvMapXY(
Rect boundingBox,
bool preserveAspectRatio,
bool mapOriginToCenter)
{
Vector2 anchor = boundingBox.position;
Vector2 size = boundingBox.size;
if (preserveAspectRatio)
{
if (size.x < size.y)
{
size = new Vector3(size.y, size.y, 0);
}
else
{
size = new Vector3(size.x, size.x, 0);
}
}
if (mapOriginToCenter)
{
return v => new Vector2(v.x / size.x + 0.5f, v.y / size.y + 0.5f);
}
else
{
return v => new Vector2((v.x - anchor.x) / size.x, (v.y - anchor.y) / size.y);
}
}
public static int GetTriangleCount(float angle, float trianglesPerRevolution)
{
return Mathf.CeilToInt(angle / (2 * Mathf.PI) * trianglesPerRevolution);
}
}
public static class MeshBuilderExtensions
{
public static List<T> Add2<T>(this List<T> list, T index0, T item1)
{
list.Add(index0);
list.Add(item1);
return list;
}
public static List<T> Add3<T>(this List<T> list, T item0, T item1, T item2)
{
list.Add(item0);
list.Add(item1);
list.Add(item2);
return list;
}
public static List<U> Differences<T, U>(this List<T> list, Func<T, T, U> difference, bool loop)
{
var result = new List<U>();
for(int i = 0; i < list.Count - 1; i++)
{
result.Add(difference(list[i], list[i + 1]));
}
if (loop)
{
result.Add(difference(list[list.Count - 1], list[0]));
}
return result;
}
/*
Gets the vector's angle in the XY plane.
*/
public static float Atan2XY(this Vector3 v)
{
return Mathf.Atan2(v.y, v.x);
}
}
public enum GLColor
{
Red,
Orange,
Yellow,
Green,
Blue,
Purple,
Magenta,
Black,
White
}
[Serializable]
public class GeometryDebug
{
public List<Vector3> dotPositions;
public List<GLColor> dotColors;
public List<Vector3> arrowPositions;
public List<Vector3> arrowDirections;
public List<GLColor> arrowColors;
public List<Color> colorMap = new List<Color>
{
Color255(255, 70, 70),
Color255(255, 150, 0),
Color255(255, 255, 60),
Color255(150, 220, 0),
Color255(25, 174, 255),
Color255(186, 0, 255),
Color255(255, 0, 193),
Color255(0, 0, 0),
Color255(255, 255, 255),
};
private static Color Color255(int r, int g, int b, int a = 255)
{
return new Color(r / 255f, g / 255f, b / 255f, a / 255f);
}
public float Radius
{
get; set;
} = 0.1f;
public GeometryDebug()
{
dotPositions = new List<Vector3>();
dotColors = new List<GLColor>();
arrowPositions = new List<Vector3>();
arrowDirections = new List<Vector3>();
arrowColors = new List<GLColor>();
}
public void Clear()
{
dotPositions.Clear();
dotColors.Clear();
arrowPositions.Clear();
arrowDirections.Clear();
arrowColors.Clear();
}
public void AddDotXY(Vector3 position, GLColor color)
{
dotPositions.Add(position);
dotColors.Add(color);
}
public void AddArrow(Vector3 position, Vector3 direction, GLColor color)
{
arrowPositions.Add(position);
arrowDirections.Add(direction);
arrowColors.Add(color);
}
public void Draw(Transform transform, MeshType meshType = MeshType.XYZ)
{
for(int i = 0; i < dotPositions.Count; i++)
{
var position = transform.TransformPoint(dotPositions[i]);
float radius = transform.lossyScale.magnitude * Radius;
Color color = colorMap[(int)dotColors[i]];
DrawDot(position, radius, color, meshType);
}
for(int i = 0; i < arrowPositions.Count; i++)
{
var position = transform.TransformPoint(arrowPositions[i]);
var direction = transform.TransformDirection(arrowDirections[i]);
float size = transform.lossyScale.magnitude * 0.2f;
Color color = colorMap[(int)arrowColors[i]];
DrawArrow(position, direction, size, color);
}
}
public static void DrawArrow(Vector3 position, Vector3 direction, float size, Color color)
{
Handles.color = color;
Handles.ArrowHandleCap(0, position, Quaternion.LookRotation(direction), size, EventType.Repaint);
}
public static void DrawDot(Vector3 position, float radius, Color color, MeshType meshType)
{
switch (meshType)
{
case MeshType.XYZ:
Gizmos.color = color;
Gizmos.DrawWireSphere(position, radius);
break;
case MeshType.XY:
Handles.color = color;
Handles.DrawSolidDisc(position, Vector3.forward, radius);
break;
case MeshType.XZ:
Handles.color = color;
Handles.DrawSolidDisc(position, Vector3.forward, radius);
break;
}
}
}